银行家算法

computer science

发布日期: 2020-04-20

文章字数: 1.1k

阅读时长: 4 分

阅读次数:

基本概念

安全状态：系统能够按照某种顺序，来为进程分配其所需的资源，如 $<p_1,p_2, \dots , p_n>$，直至每一个进程都可以顺利完成，此时系统为安全状态
安全序列：上述 $<p_1, p_2, \dots, p_n>$ 称为安全序列
不安全状态：若某一时刻系统中不存在一个安全序列，则称此时的系统状态为不安全状态

进入不安全状态之后，系统便有可能进入死锁状态

因此，避免死锁的本质是使系统不进入不安全的状态

例子：

若 $T_0$ 时刻系统的资源状态如图所示

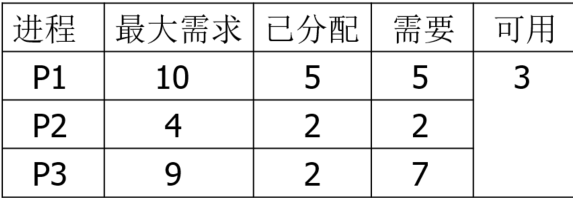
则存在一个安全状态 $<p_2, p_1, p_3>$

若 $T_0$ 时刻系统的资源状态如图所示

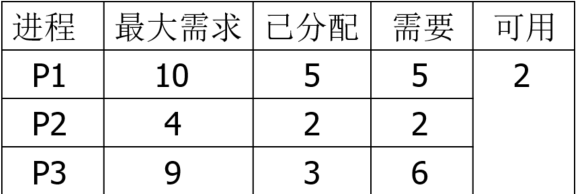
则系统处于不安全状态

算法的核心思想

资源分配后是否会导致系统处于不安全状态

数据结构

假定系统有 $n$ 个进程 $P_1, P_2, \dots , P_n$，共有 $m$ 类资源 $R_1, R_2, \dots , R_m$

可用资源向量 $Available[1 \dots m]$ ：$Available[j] = k$ 表示系统中现有空闲的 $R_j$ 类资源 $k$ 个
最大需求矩阵 $Max[1 \dots n][1 \dots m]$ ：$Max[i][j] = k$ 表示进程 $P_i$ 最多需要 $R_j$ 类资源 $k$ 个
分配矩阵 $Allocation[1 \dots n][1 \dots m]$ ： $Allocation[i][j] = k$ 表示进程 $P_i$ 已被分配 $R_j$ 类资源 $k$ 个
需求矩阵 $Need[1 \dots n][1 \dots m]$：$Need[i][j] = k$ 表示进程 $P_i$ 还需要 $R_j$ 类资源 $k$ 个
请求向量 $Request_i[1 \dots m]$ ：$Request_i[j] = k$ 表示进程 $P_i$ 请求分配 $R_j$ 类资源 $k$ 个

参与安全性算法的临时数据结构：

可用资源向量 $Work[1 \dots m]$，初值为 $Available$，含义相同，用于安全性算法
可分配向量 $Finish[1 \dots n]$，$Finish[i] = ture$ 表示有足够资源分配给进程 $P_i$

银行家算法的主要步骤

当进程 $P_i$ 发出请求向量 $Request_i$ 后，执行以下步骤

$assert \quad Request_i \le Need_i$
$assert \quad Request_i \le Available$
预分配数据结构
$$
\begin{align}
& Available = Available - Request_i \\
& Allocation_i = Allocation_i + Request_i \\
& Need_i = Need_i - Request_i
\end{align}
$$
执行安全性算法，检查此次资源分配是否安全

安全性算法的主要步骤

从进程集合中找到一个能满足下述条件的进程，找到则执行步骤2，否则执行3
- $Finish[i] = false$
- $Need_i \le Work$
当进程 $P_i$ 获得资源后，可顺利执行到完成，并释放出分配的资源，应执行
$$
\begin{align}
& Work = Work + Allocation_i \\
& Finish[i] = true \\
& goto \; step1
\end{align}
$$
若所有进程的 $Finish[i]$ 都为 $true$，则表示系统处于安全状态，否则系统处于不安全状态

例子

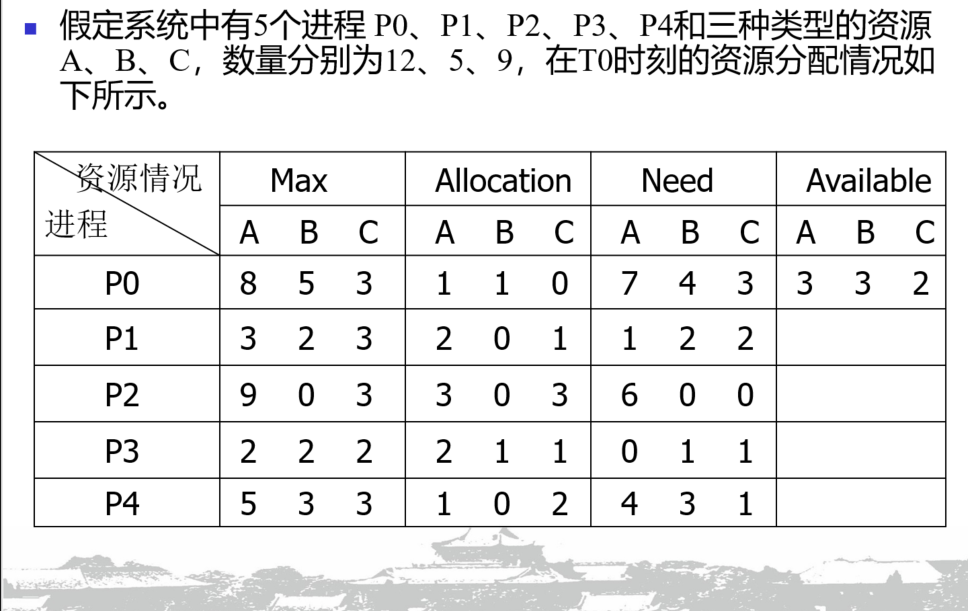
在 $T_0$ 时刻使用安全性算法，可知

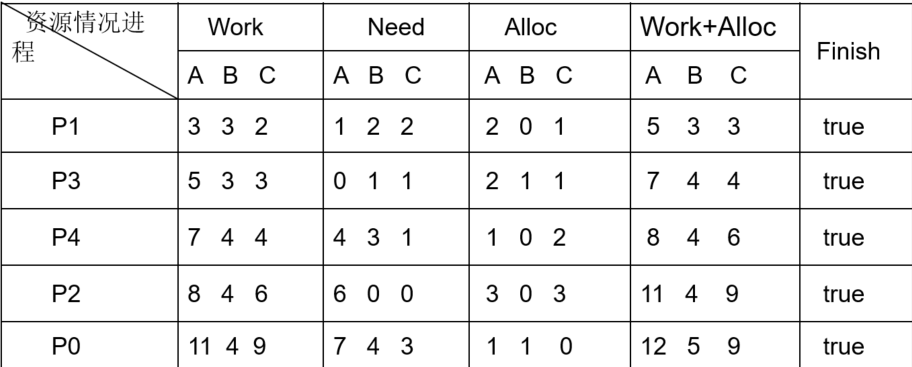
即存在一个安全序列 $<P_1, P_3, P_4, P_2, P_0>$ 因此系统是安全的

此时 $P_1$ 发出请求向量 $Request_i = \lbrace 1, 2, 0 \rbrace$，根据银行家算法，系统执行如下检查

$assert \quad Request_i \le Need_i$
$assert \quad Request_i \le Available$
为 $P_1$ 预分配资源
$$
\begin{align}
& Available = Available - Request_i \\
& Allocation_i = Allocation_i + Request_i \\
& Need_i = Need_i - Request_i
\end{align}
$$
进行安全性分析

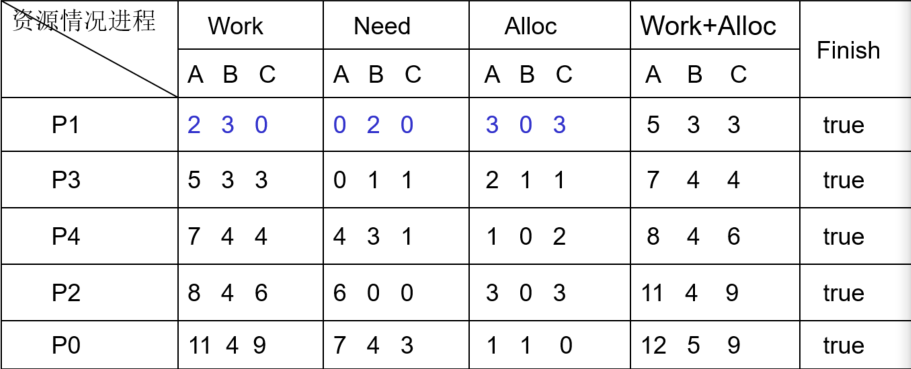
由此可知存在一个安全序列 $<P_1, P_3, P_4, P_2, P_0>$，因此系统是安全的

此时 $P_4$ 发出请求向量 $Request_4 = \lbrace 3, 3, 0 \rbrace$，可知不满足 $assert \quad Request_i \le Available$，于是进程 $P_4$ 等待

此时 $P_0$ 发出请求向量 $Request_0 = \lbrace 0, 2, 0 \rbrace$ ，可知不满足安全性检测，因此 $P_0$ 等待