出现的起因:
- 固定分区存储管理限制了内存中的进程数
- 动态分区的拼接需要大量时间
伙伴系统的主要思想
- 采用伙伴算法对空闲内存进行管理
- 该方法通过不断以 $\frac{1}{2}$ 的形式来分割大的空闲存储块,从而获得小的空闲存储块
- 当内存块释放时,应尽可能合并空闲块
伙伴系统的内存分配
- 设进程申请大小为 $n$
- 系统初始时可供分配的空间为 $2^m$
- 若 $2^{m-1} < n \le 2^m$,则为进程分配整个空间
- 若 $2^{i-1} < n \le 2^i$,则为进程分配大小为 $2^i$ 的空间
- 若系统不存在大小为 $2^i$ 的空闲块,则查找系统中是否存在大于 $2^i$ 的空闲块 $2^{i+1}, 2^{i+2} \dots$,若找到则对其进行对半划分,直到产生大小为 $2^i$ 的进程块为止
伙伴系统的内存回收
- 当一块被分成两个大小相等的块时,这两块称为伙伴
- 当进程释放存储空间时,应检查释放块的伙伴是否空闲,若空闲则合并
- 当较大的空闲块也可能存在空闲伙伴,此时也应该合并
- 重复上述过程,直至没有可以合并的伙伴
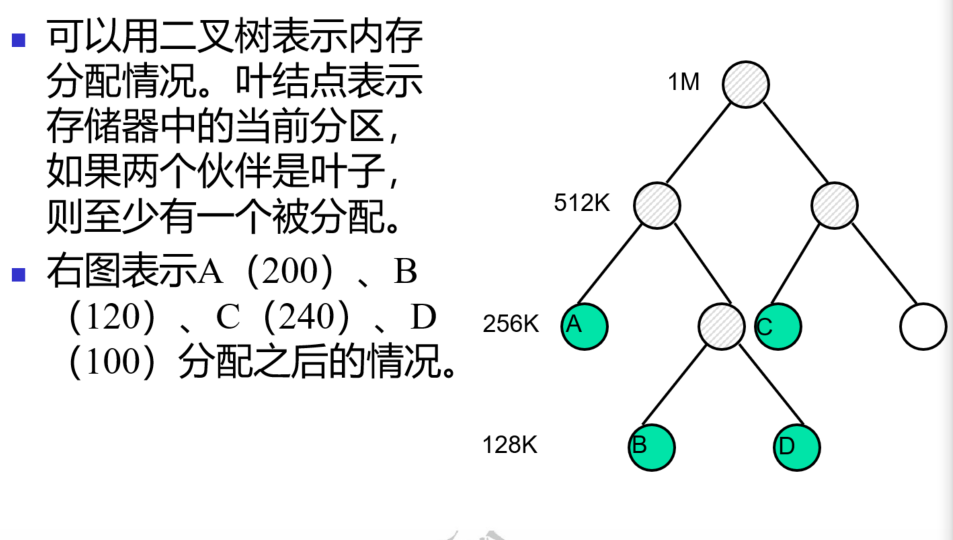
伙伴系统的二叉树表示
伙伴系统也会产生碎片
伙伴地址公式
设某空闲块的开始地址为 $d$,长度为 $2^k$,其伙伴的开始地址为(可看成已知二叉树的一个节点开始地址,求其兄弟节点开始地址(相距一个节点的长度)):
$$
Buddy(k, d) =
\begin{cases}
d + 2^k, & d \equiv 0 \quad (mod \; 2^{k+1}) \\
d - 2^k, & d \equiv 2^k \quad (mod \; 2^{k+1})
\end{cases}
$$如果参与分配的 $2^m$ 个单元从 $a$ 开始,则对于长度为 $2^k$,开始地址为 $d$ 的块,其伙伴的开始地址为:
$$
Buddy(k, d) = \begin{cases}d + 2^k, & d-a \equiv 0 \quad (mod \; 2^{k+1}) \\d - 2^k, & d-a \equiv 2^k \quad (mod \; 2^{k+1})\end{cases}
$$
例子:若块地址为 $011011110000b$,块的大小分别为 $4$ 和 $16$,则块的伙伴地址为:
加4和减16
深入理解:
- 对于两个伙伴而言,其中左节点的开始地址即为父节点开始地址,因此必能被 $2^{k+1}$ 整除,反之则为右节点
例子
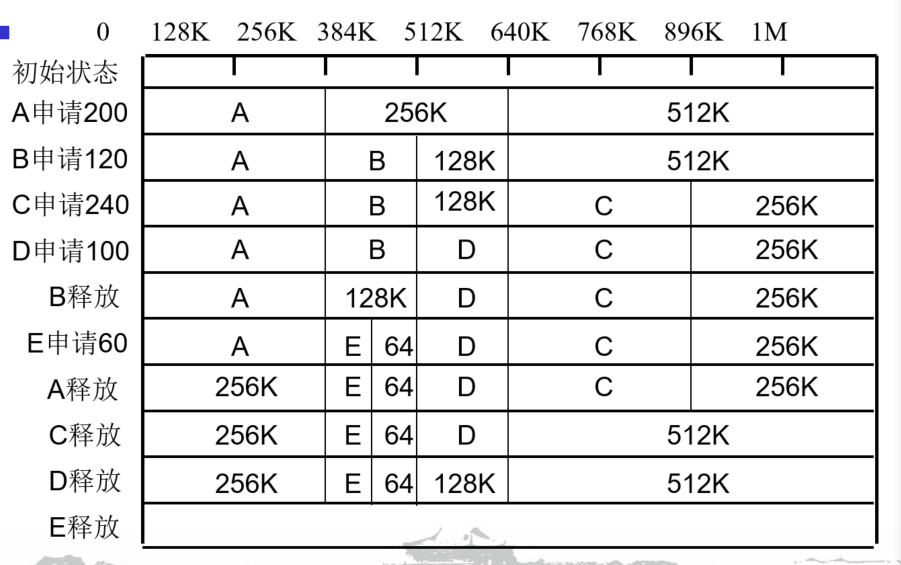
设系统中初始内存空间为 1 MB,进程请求和释放空间的操作序列为:
- 进程 A 申请 200 KB;B 申请 120 KB;C 申请 240 KB;D 申请 100 KB
- 进程 B 释放,E 申请 60 KB
- 进程 A、C 释放;
- 进程 D 释放;进程 E 释放