溢出发生的条件:
- 加法:
- 同正得负
- 同负得正
- 减法:
- 正负得负
- 负正得正
对于 MiPS 指令而言:
- 有符号数的加减法(add、sub、addi)在溢出时产生异常
- 无符号数的加减法(addu、subu、addiu)在溢出时不产生异常
addiu 在做无符号数的加法时,立即数符号扩展至32位
MIPS 使用异常程序计数器 $EPC$ 来保存导致异常的指令地址,指令 $mcf0$ 用来将 $EPC$ 存入一个通用寄存器
饱和操作是指结果发生溢出时,结果被设置为最大的正数或者最小的负数,一般用于多媒体操作
检测 MIPS 溢出举例:
对于有符号加法检测的步骤为:
- 首先判断加数和被加数的符号是否相异,如果相异则不会溢出,否则进行下一步检验
- 判断相加之后的结果于原来加数的符号是否相同
- 代码如下:

对于无符号加法的检测步骤为:
- 判断两数之和是否超过 $2^{31}-1$ ,方法为将其中一个加数取反看是否小于另一个加数
- 代码如下:
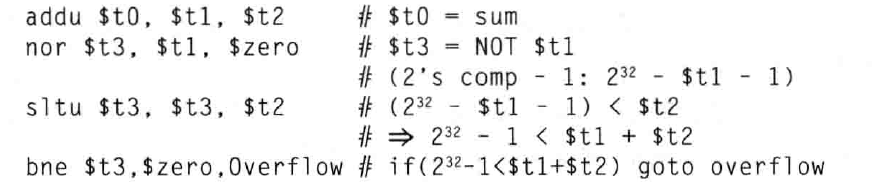
MIPS 提供了寄存器 $Hi$ 和 $Lo$ 来容纳乘法过程中 64 位的乘积,例如:
- $mult/multu \quad rs,\; rt$ 将寄存器 $rs$ 和 $rt$ 的数据相乘,乘积的低32位存入$Lo$ ,高32位存入 $Hi$
- 指令 $mul \quad rd,\; rs,\; rt$ 将 $rs$ 和 $rt$ 乘积的低32位存入寄存器 $rd$ 中
- 指令 $mfhi/mflo \quad rd$ 将 $Hi/Lo$ 的值送入寄存器 $rd$
MIPS 乘法指令都忽略溢出,需要有如软件来检测是否可能因为积过大而32位不够表示,对于 multu 指令,可以检测 Hi 的值是否为0,对于mult 指令,可以检测 Hi 的值是否为 Lo 的符号为
在有符号的除法中,必须满足等式 $被除数=商 \times 除数 + 余数$ 以及 $-(x \div y)=(-x)\div y$,因此余数的正负号的设置必须格外小心,例如:
- $-7 \div 2=-3…-1$ 而不是 $-7 \div 2 = -4…1$ (不满足后面一条性质)
提供了 $Hi$ 和 $Lo$ 来存储余数和商:
- $div \quad rs,\; rt$ 将 $rs \div rt$ 的商存入寄存器 $Lo$,余数存入寄存器 $Hi$
- $divu$ 无符号的除法
MIPS 除法指令同样忽略溢出,需要软件来检测商是否溢出
P130精解不理解
检测溢出可以用最高为的进位和次高为的进位相异或,$1 \Rightarrow Overflow \quad else \; no \; overflow$
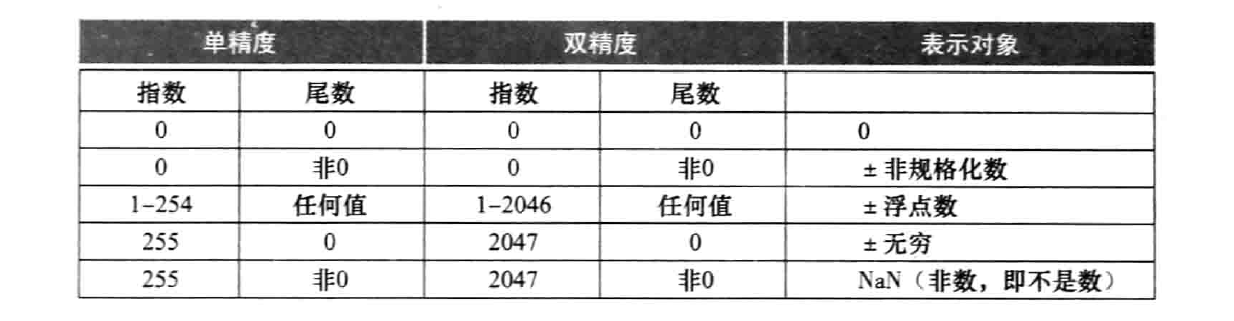
规格化数:没有前导零且小数点左边只有一位整数(如 $1.0*10^{-9}$)
MIPS 中浮点数的表示:1位符号位+8位指数位+23位尾数位(指数部分表示数的范围,尾数部分表示数的精度),MIPS 中浮点数的值可用 $(-1)^S \times (1+F) \times 2^E$ 其中 $F$ 为尾数,$E$ 为指数
浮点数的溢出:
- 上溢:正的指数太大而导致指数域放不下的情况
- 下溢:负的指数太小而导致指数域放不下的情况
浮点数的精度:
- 单精度:浮点数由一个32位的字表示(1+8+23),范围约为 $2.0 \times 10^{\pm38}$
- 双精度:浮点数由两个32位的字表示(1+11+52),范围约为 $2.0 \times 10^{\pm308}$
为了提高精度,$IEEE \quad 754$ 通常省略了前导一,即将浮点数的表示为:$(-1)^S \times (1+F) \times 2^E$ ,$F \in [0,1)$
如果从左到右标记尾数依次为 $s1, s2, s3, … ,s_t$ ,且指数的值为 $E$ ,则浮点数的值为:$(-1)^S \times [1+s_1 \times 2^{-1}+s_2 \times 2^{-2}+…] \times 2^E$
带偏阶的计数法:
- 希望计数法能将最小的负数表示为 $000…00_2$ ,最大的正数表示为 $1111…11_2$ ,我们通常在原数的基础上加上一个偏阶
- $IEEE \quad 754$ 规定单精度的偏阶为 127,例如指数为-1时,会表示成126,即 $01111110_2$ ,指数为+1时,会表示成 128,即 $10000000_2$ ;双精度额偏阶规定为 1023,给指数带偏阶之后,浮点数的表示为: $(-1)^S \times (1+F) \times 2^{E-Bias}$
求 $-0.75_{10}$ 的单精度和双精度表示:
- 单精度:{1, 01111110, 100…0}
- 双精度:{1, 011111111110, 100…0}
浮点数加法的步骤:
- 将指数较小的数向指数较大的数对齐
- 将有效数相加
- 规格化(不一定要做)
- 四舍五入(不一定要做,做了之后由于进位可能会返回步骤3)
- 例子1(假定有效位数为4): $9.999 \times 10^{1}+1.610 \times 10^{-1}$
- $1.610 \times 10^{-1} \rightarrow 0.016 \times 10^1$
- $9.999 \times 10^1+0.016 \times 10^1=10.0015\times10^1$
- $10.0015 \times 10^1=1.0015 \times10^2$
- $1.0015 \times 10^2 \rightarrow 1.002 \times 10^2$
- 例子2(假定有效位数为4):$0.5_{10}+(-0.4375_{10})$
- 两者的科学表示分别为 $1.000 \times 2^{-1}、-1.110\times2^{-2}$
- $-1.110 \times 2^{-2} \rightarrow -0.111 \times2^{-1}$
- $1.000 \times 2^{-1} + -0.111 \times 2^{-1}=0.001\times2^{-1}$
- $0.001\times2^{-1} \rightarrow 1.000 \times 2^{-4}$
- 浮点数基本结构示意图:
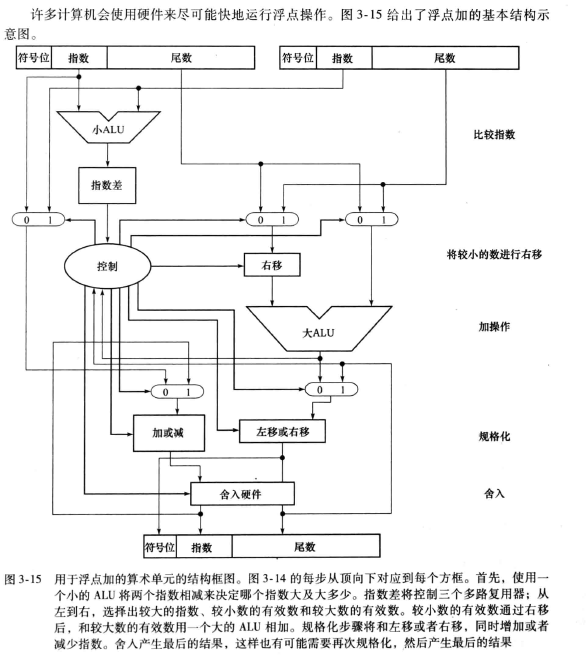
浮点数乘法的步骤:
- 将源操作数的指数相加作为积的指数(注意要减去一个偏阶)
- 计算有效数的乘法
- 规格化(检查上溢或者下溢)
- 舍入
- 积的符号相同为正,相异为负
- 例子1(假定有效位为4):计算 $0.5_{10} \times (-0.4375)_{10}$
- 二进制表示分别为:$1.000\times2^{-1}$ 和 $-1.110 \times 2^{-2}$
- 计算积的偏阶为:$-1+(-2)=-3$ (此时是没有带偏阶的,所以不需要减去偏阶)
- 将有效数相乘:$1.000 \times 1.110=1.110$,因此此时得到的结果为 $1.110 \times 2^{-3}$
- 符合规格化且没有发生溢出
- 舍入后结果不变
- 符号为 $-$
MIPS 中的浮点数指令:
- MIPS 常见的浮点数指令为:

- MIPS 中有32个32位浮点寄存器$(\$f_0,\$f_1,…,\$f_{31})$ ,单精度浮点数直接用某一个寄存器来表示,双精度浮点数由一组单精度寄存器(偶数+奇数)来表示,例如 $\$f_2,\$f_3$ 形成一个双精度寄存器,称为 $\$f_2$
- 常见的浮点数指令如图:
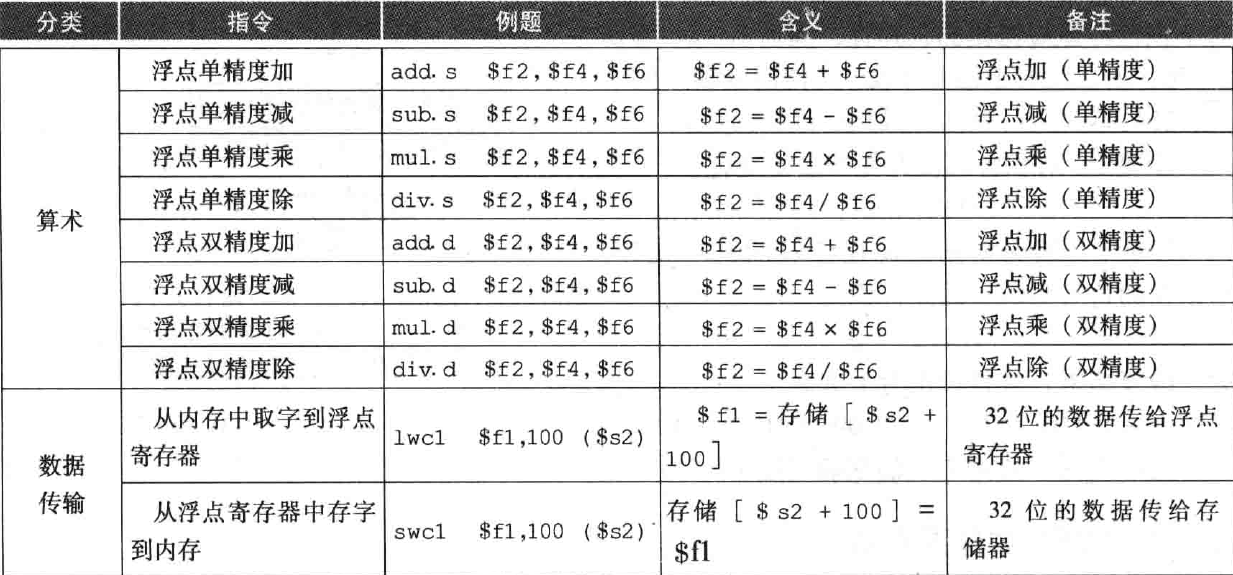
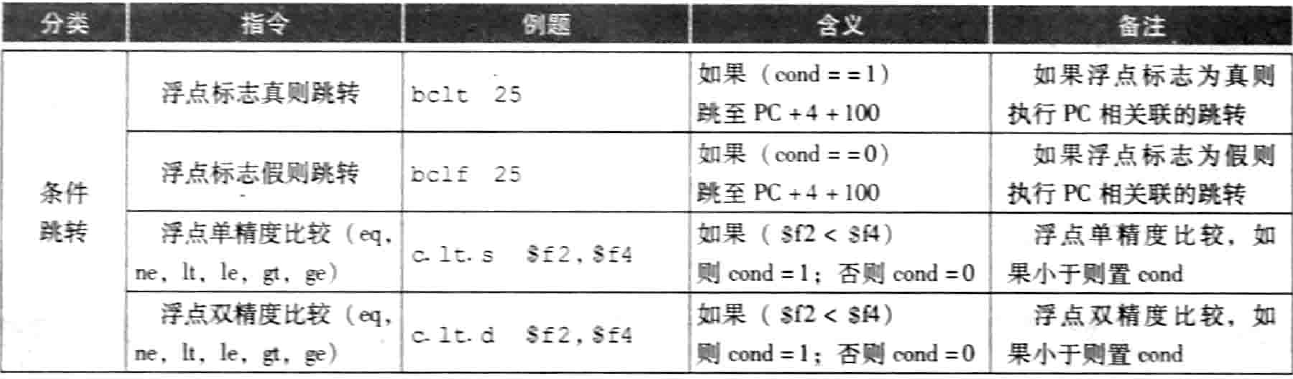
浮点算数的精确性:
- 保护位:右边多保留的第一位
- 舍入位:右边多保留的第二位
- 粘贴位:当舍入位右边有非零的数即置1,主要用于当保护位和舍入位恰好是10的情况
混合乘加指令执行一次乘法和一次加法,但只在加法后执行一次舍入,能够提高浮点性能
注意:
- 为了从一次浮点操作中最大限度的获得精度,标准允许一些数(指数最小时)以非规格化的形式出现,例如:
- 最小的正的单精度规格化数为:$1.00…0 \times 2^{-126}$
- 最小的正的单精度非规格化数为:$0.000…1\times2^{-126}$
- 左移指令可以代替2的幂次方数相乘,右移指令不能代替2的幂次方数相除(对于无符号整数是对的,但是对于有符号整数不一定正确(负数可能变成正数))
- 浮点数加法没有结合律(例如$c=-1.5 \times 10^{38},a=1.5\times10^{38},b=1.0$,则$c+(a+b)=0$ 而 $(c+a)+b=1$)



